Henryk Iwaniec
| Henryk Iwaniec | |
|---|---|
| Born | October 9, 1947 Elbląg, Poland |
| Residence | United States |
| Citizenship | United States |
| Fields | Mathematician |
| Institutions | Polish Academy of Sciences Institute for Advanced Study Rutgers University |
| Alma mater | University of Warsaw |
| Doctoral advisor | Andrzej Schinzel |
| Known for | analytic number theory Bombieri–Friedlander–Iwaniec theorem automorphic forms Sieve theory |
| Notable awards | 2001 Ostrowski Prize 2002 Cole Prize 2011 Steele Prize |
Henryk Iwaniec (born October 9, 1947) is a Polish American mathematician, and since 1987 a professor at Rutgers University. He was awarded the fourteenth Frank Nelson Cole Prize in Number Theory in 2002. He received the Leroy P. Steele Prize for Mathematical Exposition in 2011.
Contents |
Background and education
Iwaniec studied at the University of Warsaw, where he got his Ph.D. in 1972 under Andrzej Schinzel. He then held positions at the Institute of Mathematics of the Polish Academy of Sciences until 1983 when he left Poland. He held visiting positions at the Institute for Advanced Study, University of Michigan, and University of Colorado at Boulder before being appointed Professor of Mathematics at Rutgers University. He is a citizen of both Poland and the United States. [1]
Work
Iwaniec is well-known for his proficiency in both sieve methods and deep complex-analytic techniques, with a particular emphasis on the theory of automorphic forms and harmonic analysis.
In 1997, Iwaniec and John Friedlander proved that there are infinitely many prime numbers of the form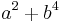 
.[2] Results of this strength had previously been seen as completely out of reach: sieve theory—used by Iwaniec and Friedlander in combination with other techniques—cannot usually distinguish between primes and products of two primes, say.
In 2001 Iwaniec was awarded the seventh Ostrowski Prize.[3] The prize citation read, in part, "Iwaniec's work is characterized by depth, profound understanding of the difficulties of a problem, and unsurpassed technique. He has made deep contributions to the field of analytic number theory, mainly in modular forms on GL(2) and sieve methods."[3]
Publications
- Iwaniec, Henryk (1997). Topics in Classical Automorphic Forms. Providence: American Mathematical Society. ISBN 9780821807774.
- Iwaniec, Henryk (2002). Spectral Methods of Automorphic Forms (2nd ed.). Providence: American Mathematical Society. ISBN 9780821831601.
- Iwaniec, Henryk; Emmanuel Kowalski (2004). Analytic Number Theory. Providence: American Mathematical Society. ISBN 9780821836330.
- Iwaniec, Henryk; J. B. Friedlander, D. R. Heath-Brown, J. Kaczorowski (2006). Analytic Number Theory: Lectures Given at the C.I.M.E. Summer School Held in Cetraro, Italy, July 11–18, 2002. Berlin: Springer. ISBN 9783540363637.
- Friedlander, John; Iwaniec, Henryk (2010). Opera de Cribro. Providence: American Mathematical Society. ISBN 9780821849705.
References
- ^ "2002 Cole Prize in Number Theory". Notices of the American Mathematical Society (Providence: American Mathematical Society) 49 (4): 476–478. April 2002. ISSN 0002-9920. http://www.ams.org/notices/200204/comm-coleprz.pdf.
- ^ Friedlander, John; Iwaniec, Henryk (1997). "Using a parity-sensitive sieve to count prime values of a polynomial". PNAS 94 (4): 1054–1058. doi:10.1073/pnas.94.4.1054. PMC 19742. PMID 11038598. http://www.pnas.org/content/94/4/1054.abstract.
- ^ a b "Iwaniec, Sarnak, and Taylor Receive Ostrowski Prize"
Further reading
- Cipra, Barry (1998). "Sieving Prime Numbers From Thin Ore". Science 279 (5347): 31. doi:10.1126/science.279.5347.31.